はじめてのにき

_ GC

なんか gus さんの最初の直感、

http://twitter.com/gusmachine/status/18877553931

は Ruby と Haskell に関しては 正しいんじゃないかなぁとか思えてきたんだ…

まず世代を忘れる。 仮に領域を確保するたびに GC が走るアホ GC があったとして、 今回のプログラムはメモリの解放は起きないので、 copying だろうと mark and sweep だろうが 一回の GC の走査量はたかだか N^2 。 それが N 回起きるので O(N^3) になって、 これが最悪のオーダーで、 O(N^2) の領域使ってるんだから O(N^2) 以上はかかるでしょ、 という理由で最小 O(N^2) なので、 まぁ O(N^2) から O(N^3) のどこかにおさまるべきでしょう。

ところで今回のプログラムは、 確かにメモリは N^2 使うんだけど、 オブジェクトの数はたかだか 2N 個しか無い。 だから一回の mark and sweep GC の 走査量は O(N) なんじゃないだろうか。 だとすると仮に毎度 GC 走るアホ GC だとしても、 たかだか O(N^2) じゃね？

…というような理由で、 Ruby の O(N^2.47) が謎に思えてきた。

次に Haskell 。 Haskell はそもそも普通に GC しててメモリ消費量は O(N) なので、 何がどうなってようがたかだか O(N^2) なんじゃなかろーか。

最後に D は、これも mark and sweep なんだろうけど、 コンサバなもんですから、 O(N^2) の空間なめちゃうんじゃないか (Ruby は BigNum の中はなめないよね?)。 つまり、仮にアロケーションのたびに GC が走ってたなら O(N^3) になりうる。

あとはどのくらいの頻度で GC が起きるかってのが問題。 単純に vector みたいに倍々で増やしてたりすれば O(N^2) になるはず。 D の gcx.d とかをチラ見するに、

• 4k 以上の allocation (たぶん今回はほぼこれだろう) は bigAlloc を通りそう
• bigAlloc は既存の pool を巡回して、空いてるのが無ければ full GC => それで足りなければ newPool
• つーわけで newPool 時に allocation するサイズが問題である
• newPool をざっくり読む
  • まず確保する page 数を今欲しい数の 1.5 倍にする
  • で、 pool の数が 2 個目だと最低でも 2MB 、 次は 3MB …となって、 8 個を越えると固定で 16MB, 32 個を越えると 32MB って感じで pool 最小値を決めていく
  • 32 個を越える段階では 400MB とか allocate してることになる気がするので、結局数 MB から 16MB 程度の allocation をしていく、ってことになるんじゃないかと思う

で、定数ずつ allocation していくとか、 2,3,4,... という感じで定数ずつ allocation する量が増えていく、ってやり方だとあっさり O(N^3) になるわけだけど、数 MB 単位で allocation してるなら、そもそも今回のベンチマーク程度だと、 GC が起きる総数がそんなに多くないので、 O(N^2) の方が十分に強くて、間くらいのオーダーに見えた、ってのはアリかなー。

適当に simulation を書いてみた。

#!/usr/bin/env ruby

use_size = 0
heap_size = 1000000
next_gap = 1000000
num_gcs = 0

simulated_time = 0
gc_time = 0
calc_time = 0

1.upto(100000) do |n|
  use_size += n / 20
  if use_size > heap_size
    while use_size >= heap_size
      heap_size += next_gap

      #next_gap = heap_size
      #next_gap = Math.sqrt(heap_size).to_i
      #next_gap += Math.sqrt(next_gap).to_i
      #next_gap += 100
      if next_gap <= 8000000
        next_gap += 1000000
      else
        next_gap = 16000000
      end
    end

    # Time for GC.
    num_gcs += 1
    gc_time += use_size
    simulated_time += use_size
  end

  calc_time += n / 2.5
  simulated_time += n / 2.5

  puts "#{n} #{simulated_time}" if n % 100 == 0
end

STDERR.puts heap_size / 1024 / 1024
STDERR.puts num_gcs
STDERR.puts gc_time
STDERR.puts calc_time

calc_time を増やす時にかかっている /2.5 は、 gc_time と calc_time をだいたい同じにする程度に normalize している。

これを fit すると O(N^2.55216) とのこと。 この指数は / 2.5 の部分を適当に調整すると色々変わる。

グラフはこんな感じ

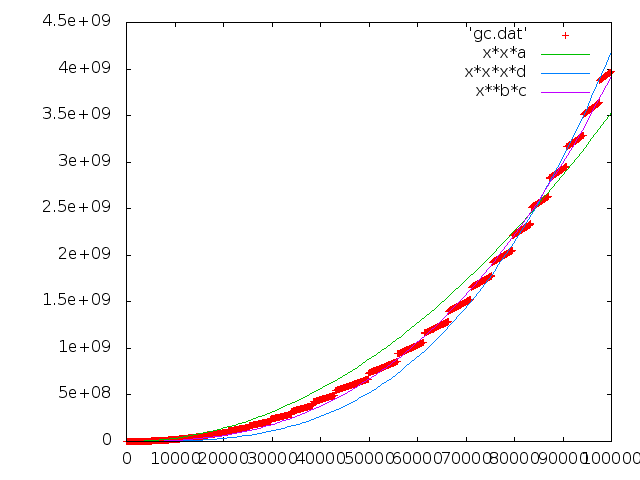
つーわけで、 D に関しては実は O(N^3) なんだけど、 GC が適当に現実的なメモリに対してでかいと 考えられる単位で allocation しているので、 GC 頻度が少なく、 O(N^3) の係数が十分に少ないために O(N^2.5833) とかに見えた、って説はどうだろう。

実際数えてみた。 gdb で fib を走らせて、 _D2gc3gcx3Gcx16fullcollectshellMFZk に break 仕込んで cont 連打。N==100000 で 39 回とのこと。 上の simulation コードは 22 回だと言ってるのでそれなりに回数にずれがあるけど、 いずれにせよこんだけ少ない回数しか O(N^2) の operation が起きてないんなら O(N^3) に見えなくても納得できる感じかな。

あと上のコードの next_gap を色々調整してるうちに 気付いたんだけど、 next_gap += Math.sqrt(next_gap) 的な 増やしかたをしていると、 なんか O(N^2.6) あたりになる。 でもまぁそいう実装になってないっぽいのであんま関係なさげ。

(00:35)

_ 39 回の fullcollect

以下は、左から、 GC の回数、その GC の時 fib のどこを計算してたか、前回との差分、って感じ

1 3686 3686
2 5775 2089
3 7165 1390
4 10228 3063
5 13058 2830
6 15618 2560
7 18690 3072
8 22274 3584
9 24939 2665  // ここから毎回 bigAlloc によって fullcollect が呼ばれるようになった
10 29035 4096
11 33131 4096
12 37227 4096
13 41323 4096
14 45419 4096
15 48265 2846
16 50313 2048
17 52361 2048
18 54409 2048
19 56457 2048
20 58023 1566
21 59958 1935
22 62091 2133
23 64139 2048
24 66187 2048
25 68235 2048
26 70283 2048
27 72331 2048
28 74379 2048
29 76427 2048
30 78475 2048
31 80523 2048
32 82571 2048
33 84619 2048
34 88715 4096
35 92811 4096
36 96009 3198
37 98739 2730
38 99999 1260

最初の 1 回はプログラム開始時みたいなタイミングで呼ばれてたので除外。

うーんやたら定期的に呼ばれすぎ感が。 なんかおかしいなぁ。

(01:07)

_ あと

Ruby とか Haskell とかは実は GC とかまるで関係なくて 多倍長整数の実装のしかたとかそのへんが関係してるとか無いもんか

(01:08)

_ shortest

http://blog.hackers-cafe.net/2010/07/shortest-oneline-brainfck-interpreter.html

いくら one liner でも 558B で shortest はたぶん無いなー。

python one liner ってのは面白いネタだと思うんだけど、 ただ exec は封印しないと全く意味ない縛りになっちゃうよなぁ。

とりあえず codegolf.com の top は 200 切ってるし、 僕が適当に書いても 335B とかで書けて、 exec 使って one liner にしたら 362B 。 さてこれをファイルから読むとかやっても 400B にはならんだろーから、 まぁ少なくとも exec 使うのは自粛すべきだな。

で、最短の bf インタプリタって常識的に考えて… っていう意味で矛盾がまたあるんだが。

(01:28)

_ そっちはどでもよくて

http://blog.hackers-cafe.net/2010/07/haskell-quiz-answer.html

こっちは大変勉強になったのだった。 なるほど a とか b の overload ってのができるんだなあ

(01:31)